Cours de Math. 1^èreES du 20 Mai 2014 Dérivées

• Fonction f(x) = x⁴ − 4 x³ − 2 x² + 12 x + 1
  • représentation C_f de f(x) :
    
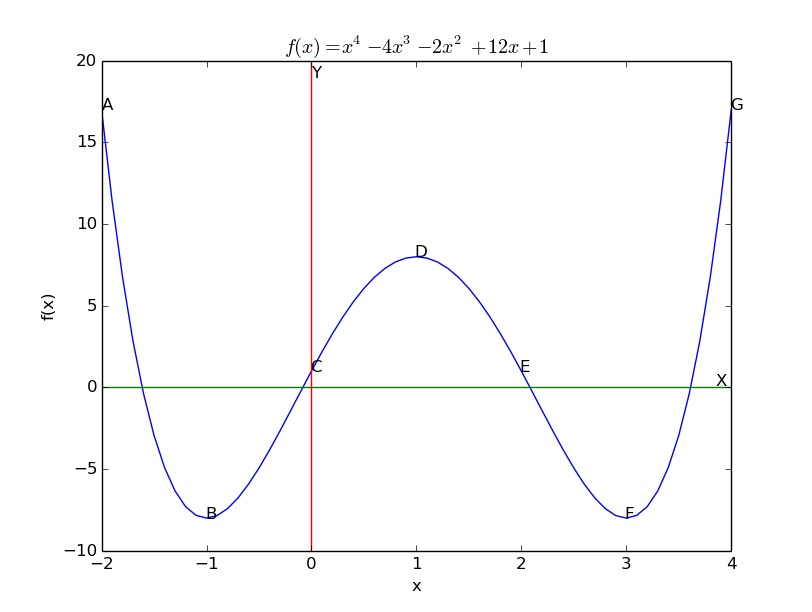
  • On donne :

    points	A	B	C	D	E	F	G
    x	−2	−1	0	1	2	3	4
    f(x)	17				1	−8
    f '(x)	−60	0		0		0

  • D'après la courbe représentative de f(x), dresser le tableau de signe de sa dérivée f '(x)
  • dresser un tableau de variation approximatif de f '(x) :
    on appellera (x₁, y₁) et (x₂, y₂) les maximum et minimum locaux de f '(x)
  • résoudre l'équation f '(x) = 0
  • Calculer les intersections de la tangente en A (−2, 17) avec les axes Ox et Oy
  • La tangente en E à C_f passe par le point (0, 25) en déduire son équation.
  • Calculer sa dérivée f '(x)
  • On appelle g(x) la fonction f '(x) :
    • calculer la dérivée g'(x)
    • étudier son signe
    • en déduire le tableau de variation de g(x)
    • que représentent les maximum et minimum locaux de g(x) = f '(x) ?
• Calculer les expressions suivantes
  • A = ( 1 + 1/n ) ( 1 − 1/(n+1) ) = ?
  • B = ( 1 − 1/n ) ( 1 + 1/(n−1) ) = ?
  • Comment interpréter ces 2 relations en terme de taux d'évolution ?

retour au menu : cours 2013   cours 2008   math 1ère ES   math