DM du 27/09/2020 [répertoire]

• exercice 1 : Intervalle de définition : [−8 ; 0] ou Domaine de définition
  • 1) tableau de variation de g :

    x	−8		−5		−2		0
    x	3	↘	−1	↗	4	↘	2

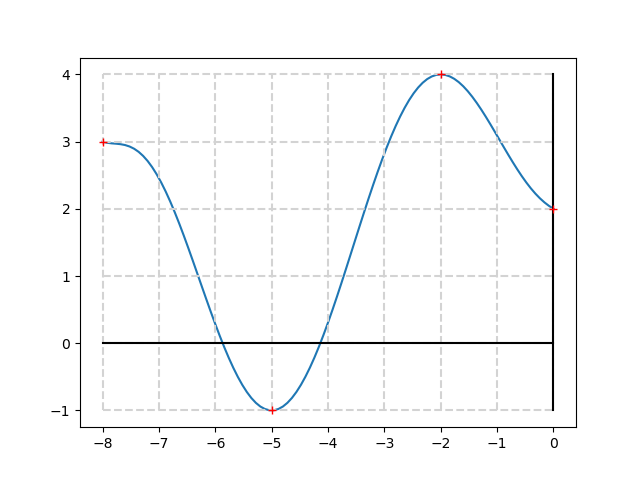
  • 2) courbe possible :
    
    Rappel :
    antécédent(y) : x →(f)→ y : image(x) = f(x)
    si l'antécédent(y) est unique, on le note x = f⁻¹(y)   (avec f⁻¹ fonction réciproque de f)
    fonction croissante     : a < b ⇒ f(a) < f(b)   l'ordre des images est le même que l'ordre des antécédents
    fonction décroissante : a < b ⇒ f(a) > f(b)   l'ordre des images est le contraire de l'ordre des antécédents
    fonction monotone : fonction toujours croissante ou toujours décroissante.   a ≠ b ⇒ f(a) ≠ f(b)
  • 3) sur l'intervalle [−7 ; −6] : g ↘ :
    −7 < −6 ⇒ g(−7) > g(−6)
  • 4) sur l'intervalle [−3 ; −1] : g ↗ puis ↘ :
    on ne peut pas comparer g(−3) et g(−1)
  • 5) −3 ∈ ]−5 ; −2[   →(f)→   ]−1 ; 5[ :
    donc g(−3) ∈ ]−1 ; 5[ : le signe de g(−3) est indéterminé
  • −1 ∈ ]−2 ; 0[   →(f)→   ]2 ; 4[ :
    donc g(−1) ∈ ]2 ; 4[ : g(−1) > 2 donc g(−1) est positif
• exercice 2 : Intervalle de définition : [−5 ; 4] ou Domaine de définition
  • a) par lecture graphique : f(−4) = 0
  • b) f(−1) = 3
  • c) antécédents de 0 :
    f(−4)=0 ; f(1)=0 ; f(3)=0   les antécédents de 0 ∈ {−4 ; 1 ; 3 }
  • d) f(x) = 2 : recherche des points d'intersection de la courbe avec la droite y=2
    S = {−3, 0} ⊂ [−5 ; 4]
  • e) f(x) = 1 : a 3 solutions dans [−5 ; 4]
    une solution ∈ [−4 ; 3], une autre ∈ [0 ; 1], une dernière = 4
  • f) maximum = (−1,3) ; l'abscisse du maximum est x=−1 ∈ [−5 ; 4]
    point de plus grande ordonnée (le plus haut) de la courbe
  • g) f(x) ≥ 2 : on recherche l'ensemble des points situés au-dessus de la droite y=2
    S = [−3 ; 0]
  • h) minimum = (2,−2) ; l'abscisse du maximum est x=2 ∈ [−5 ; 4] de valeur y=−2
    point de plus petite ordonnée (le plus bas) de la courbe
  • i) tableau de variation

    x	−5		−1		2		4
    x	−1	↗	3	↘	−2	↗	1

  • j) tableau de signe

    x	−5		−4		1		3		4
    x	−		0	+	0	−	0	+

• exercice : (1−4x) / (x² + x + 1) ≤ 0 :
  étude de signe d'un quotient ou d'un produit :
  étude de (1−4x) : 1−4x=0 ⇒ x=1/4 du signe de a=−4 pour x→+∞   (à droite)
  étude de (x² + x + 1) : Δ=b²−4ac = 1 − 4 = −3 < 0 : toujours du signe de a=1

  x	−∞		1/4		+∞
  signe(1−4x)	+		0	−
  signe(x2 + x + 1)	+		+	+
  signe(quotient)	+		0	−

  S = [ 1/4 ; +∞ [
• Convertir des nombres : binaires, hexadécimaux, décimaux
  • apprendre-en-ligne.net bases.html
  • 1) binaires   ↔   hexadécimaux :
    on regroupe les binaires par 4 :
    correspondance : . . .
    8_H= 8_D=1000_b ; 9_H= 9_D=1001_b
    A_H=10_D=1010_b ; B_H=11_D=1011_b
    C_H=12_D=1100_b ; D_H=13_D=1101_b
    E_H=14_D=1110_b ; F_H=15_D=1111_b

    binaire	0110	1010	1111	0010
    hexadécimal	6	A	F	2

  • 2) convertir un nombre binaire en décimal :

    position n	10	9	8	7	6	5	4	3	2	1	0
    2n	1024	512	256	128	64	32	16	8	4	2	1
    nombre binaire	1	0	0	1	1	0	1	1	1	0	1

    nombre décimal = 1024 + 128 + 64 + 16 + 8 + 4 + 1 = 1245_D
  • 3) convertir un nombre décimal en binaire : 2300_D
    on cherche entre quelles puissances de 2 se trouve ce nombre :

    211	=	2048	≤	2300	<	212	=	4096
    2300 − 2048 = 252
    2 7	=	128	≤	252	<	2 8	=	256
    252 − 128 = 124
    2 6	=	64	≤	124	<	2 7	=	128
    124 − 64 = 60
    2 5	=	32	≤	60	<	2 6	=	64
    60 − 32 = 28
    2 4	=	16	≤	28	<	2 5	=	32
    28 − 16 = 12
    2 3	=	8	≤	12	<	2 4	=	16
    12 − 8 = 4
    2 2	=	4	≤	4	<	2 3	=	8
    4 − 4 = 0

    2300_D = 2¹¹ + 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2²
    nombre_b = 100011111100_b
    nombre_b = 1000 1111 1100_b
    nombre_H = 8 F C_H
  • 3bis) autre méthode (plus simple) : 2300_D

    2300 / 2	=	1150	reste 0	(20)
    1150 / 2	=	575	reste 0	(21)
    575 / 2	=	287	reste 1	(22)
    287 / 2	=	143	reste 1	(23)
    143 / 2	=	71	reste 1	(24)
    71 / 2	=	35	reste 1	(25)
    35 / 2	=	17	reste 1	(26)
    17 / 2	=	8	reste 1	(27)
    8 / 2	=	4	reste 0	(28)
    4 / 2	=	2	reste 0	(29)
    2 / 2	=	1	reste 0	(210)
    1 / 2	=	0	reste 1	(211)

    nombre = 2¹¹ + 2⁷ + 2⁶ + 2⁵ + 2⁴ + 2³ + 2²
    le nombre binaire est formé des restes du dernier au premier : 100011111100_b
  • conversion en hexadécimal :

    2300 / 16	=	143	reste	12=C
    143 / 16	=	8	reste	15=F
    8 / 16	=	0	reste	8=8

    nombre hexadécimal = 8 F C_H

retour au menu :   cours 2020-2021   math 1ère S   math