exercices (de votre livre de cours) ou :
https://www.lyceedadultes.fr/sitepedagogique/pages/math1S.html
cours vidéo : https://www.maths-et-tiques.fr/
- révision des vecteurs : m@ths et tiques
https://www.maths-et-tiques.fr/index.php/cours-maths/niveau-seconde#6
Cours sur les vecteurs (pdf)
Vidéo : LE COURS : Vecteurs et repérage - Seconde
Vidéo : Déterminer les coordonnées d'un point défini par une égalité vectorielle - Seconde - m@ths et tiques : Calculer un produit scalaire à l’aide du cosinus - Première
- Soient 2 points A et B. Vecteur déplacement de A à B : u = AB
plan affine : avec les points du plan : A, B, C, O
espace vectoriel : tous les vecteurs u, v, w partent de l'origine O
il y a un espace vectoriel en chaque point de l'espace
vecteur u = AB ≠ segment [AB] : un vecteur u part de l'origine de son espace vectoriel
quand on l'utilise, on prend comme origine un point quelconque du plan
les vecteurs sont représentés partant de l'origine O
exemple de plusieurs champs électriques en un point de l'espace : espace vectoriel en ce point
exemple de plusieurs forces appliquées en un point de l'espace : espace vectoriel en ce point - addition des vecteurs : AB + BC = AC (relation de Chasles)
devient u + v = w en mettant v au bout de u
2 déplacements dans des directions différentes = déplacement résultant AC - vecteurs opposés : 2 déplacement opposés = déplacement nul : AB + BA = AA = 0
BA = − AB
quand on a un vecteur u, on obtient le vecteur −u en le retournant par rapport à son origine - proportionalité : AC = k AB quand k varie sur ℝ on obtient une droite de direction AB
droite du plan passant par A et de vecteur directeur u : décrite par le point M : AM = k u k décrivant ℝ - égalité : AB = CD : en déplaçant u = CD en A, u se supperpose à AB
ABDC forme un parallélogramme - longueur d'un vecteur u : noté ||u|| comme les valeurs absolues (2 fois)
- Base orthonormée : (i, j)
ortho = orthogonal : i ⊥ j
norme = longueur : longueur(i) = ||i|| = ||j|| = 1
un vecteur peut toujours être représenté dans cette base par 2 nombres x et y : u = x i + y j
longueur ou module d'un vecteur comme i ⊥ j : Pythagore : (x i)² + (y j)² = u² = ||u||²
comme ||i|| = ||j|| = 1 : x² + y² = u² = ||u||²
||u|| = √x² + y²
Vidéo : m@ths et tiques : LE COURS : Trigonométrie - Première
fiche : http://freescience.fr/math/trigonometrie/index.html
triangle rectangle en A = ABC : hypothénuse BC opposée à l'angle droit
Pythagore AB² + AC² = BC²
sinus: sin(B) = côté opposé / hypothénuse = AC / BC
cosinus: cos(B) = côté adjacent / hypothénuse = AB / BC
tangente : tan(B) = côté opposé / côté adjacent = AC / BA = sin(B) / cos(B)
cercle trigonométrique : rayon = 1
http://freescience.fr/math/trigonometrie/cercle_trigo.html
les coordonnées d'un point M du cercle sont : x = cos(α) et y = sin(α)
cos(0) = 1 ; sin(0) = 0
Pythagore : x² + y² = r² = 1 donc : cos²(α) + sin²(α) = 1
Calculer une probabilité à deux épreuves à l'aide d'un arbre (2) - Première
habituellement une variable x prend une valeur unique : x = 3
la longueur mesurée d'une table = 1,200 m
mais il y a des incertitudes : précision de la mesure, dilatation du mètre avec lequel on mesure
quand on prend plusieurs mesures, on trouve des résultats légèrement différents
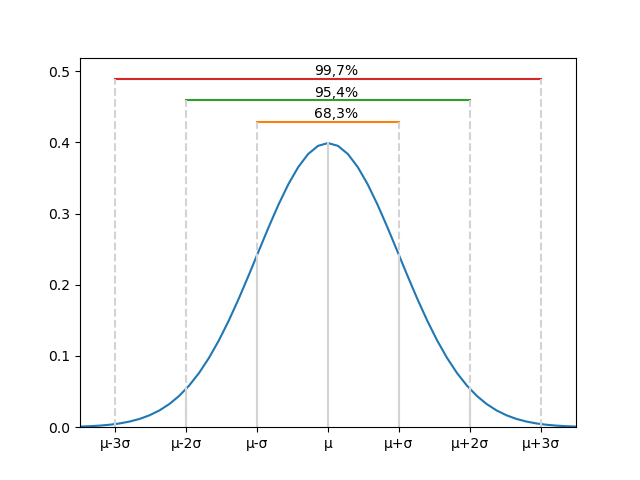
pour la longueur, on a une distribution
| longueur | 1,198 | 1,199 | 1,200 | 1,201 | 1,202 |
| nb mesures | 2 | 8 | 15 | 10 | 3 |
probabilité(longueur = 1,198) = 2 / 38
probabilité(longueur = 1,199) = 8 / 38