Cours du 08/01/2021   ([répertoire])   − ↗ → ↘ √ ∞ ℝ × ∈

• dérivée et sens de variation : dérivée = "coefficient directeur"/"pente"/"inclinaison" de la tangente
  en vélo sur la route : la route monte ↗, est plate → ou descend ↘
  ≡ la fonction hauteur(x) est croissante ↗ est stationnaire → ou est décroissante ↘

  f '(x) > 0 : f(x) ↗

  f '(x) = 0 : f(x) →

  f '(x) < 0 : f(x) ↘

• exercice 7 : g(x) = x − 4 √x
  tracer la courbe g(x)
  g'(x) = 1 − 4 / (2 √x) = 1 − 2 / √x
  signe de g'(x) : factorisation g'(x) = (√x − 2) / √x
  signe de (√x − 2) ?
  pour une fonction f ↗   ⇒   signe(a − b) = signe(f(a) − f(b))
  la fonction carré (x²) est ↗ sur ] 0 ; ∞ [ donc signe(a − b) = signe(a² − b²)
  signe de (√x − 2) = signe de (x − 4)
  g'(4) = 0   ;   g(4) = 4 − 4 × 2 = −4

  x	0		4		∞
  g'(x)	||	−	0	+
  g(x)	0	↘	−4	↗	∞

  passage à 0 dans l'intervalle ] −4 ; ∞ [ : g(x) = 0 pour (√x − 4) = 0
  √x = 4     x = 16   :   g(16) = 0
  a) FAUX : g(1) = −3
  b) FAUX : g(4) est un minimum
  g(x) n'a pas de maximum car : limite de g(x) = ∞   quand x → ∞
  car g(x) = x − 4 √x = √x (√x − 4)
  quand x → ∞ : limite de √x = ∞ et limite de (√x − 4) = ∞
  donc limite de g(x) = ∞ × ∞ = ∞
  c) FAUX : g(4) = −4
  d) VRAI : g ↗ sur [ 4 ; ∞ [ car g'(x) > 0 sur ] 4 ; ∞ [
• f(x) = 1/x : coupure en x=0 : ↘ pour chaque branche, mais pas sur un intervalle [−a, +a]
  f(x) = 1/x ↘ sur ]−∞ ; 0[ et sur ]0 ; ∞[

  x	−∞			0			∞
  g'(x)	−			||	+
  g(x)	0	↘	−∞	||	∞	↘	0

  bien que f(x) soit toujours ↘ : f(−1) < f(1)
  au passage à la coupure x=0, la fonction 1/x fait un saut infini de −∞ à +∞
• f '(x) = 0 : maximum ou minimum ou méplat
  extremum : maximum ou minimum
  maximum (↗→↘) minimum (↘→↗)
  méplat : dans une montée (↗→↗) ou dans une descente (↘→↘)
• Pourquoi parlent-ils toujours d'intervalles ouverts ?
  rappel :
  intervalle ouvert ]a, b[ ; intervalle fermé [a, b] ; ni ouvert ni fermé : ]a, b] ou [a, b[
  intervalle ouvert ]a, b[ : pour avoir une dérivée des 2 côtés du point
  Tout point de l'intervalle ouvert est entouré d'autres points (voisinage à gauche et à droite)
  ℝ est-il un intervalle ouvert ? OUI ℝ = ]−∞ ; +∞[
• On peut avoir un point d'inflexion avec f '(a) = 0 sans que ce soit un minimum ou un maximum
  Quelle fonction simple illustre ce cas ? x³
• Une fonction peut être définie de 2 manières :
  1) graphiquement : pour chaque x, on a f(x) à lire sur le graphique (équivaut à un tableau infini)
  on voit alors aussi sa dérivée f '(x) sur le graphique
  1 bis) Dans le cas d'une fonction discrète, on peut la représenter par un tableau
  2) analytiquement : on donne la formulation de f(x)
  il faut alors calculer sa dérivée f '(x)
• fonction continue : sans saut
  Au bord d'un intervalle fermé [a, b] : en b, la fonction est continue et dérivable seulmement à gauche.
  fonction dérivable : la dérivée est définie (pas infinie)
  la même à gauche et à droite (pas d'angle dans la courbe)
• Soit la courbe f(x) suivante :
  
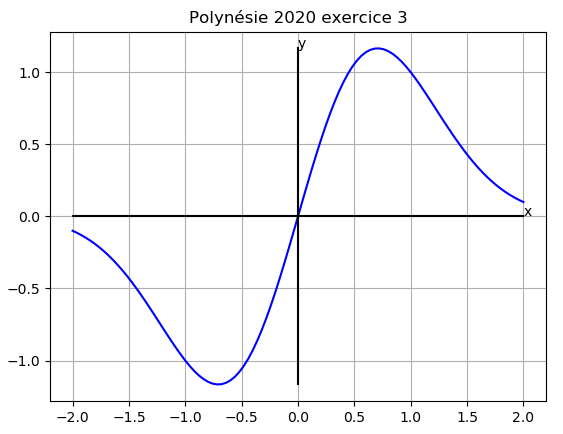
  1) déterminer son tableau de variation (à la précision de 0,1)

  x	−2		−0,7		0		0,7		2
  g'(x)	−		0	+	0	+	0	−
  g(x)	↘		−1,2	↗	0	↗	1,2	↘

  2) résoudre l'équation f(x) = 0,5
  intersection de la courbe avec l'horizontale y=0,5 : S = { 0,2 ; 1,4 }
  3) résoudre l'inéquation f(x) ≥ 0,5
  x ∈ [ 0,2 ; 1,4 ]
• 4 exercices :
  à partir de la courbe de f
  à partir de la courbe de f '
  de la fonction f(x)
  de la fonction f '(x)
• tracer une fonction : sur un intervalle ouvert
  croissante / décroissante
  avec un maximum et un minimum et une tangente horizontale non extremum
  croissante // croissante avec une coupure

retour au menu :   cours 2020-2021   math 1ère S   math