- la forme canonique : f(x) = a (x − xs)² + y
s
idéale pour étudier la courbe : sommet (xs, ys)
courbe en forme de ∪ si a > 0 et en forme de ∩ si a < 0
f(x) = a (x + b/(2a))² − Δ/(4a) : xs = −b/(2a) et ys = −Δ/(4a) - la forme développée : f(x) = a x² + b x + c
idéale pour calculer les points- la forme factorisée : f(x) = a (x − x1) (x − x2)
idéale pour les racines : f(x) = 0 pour x ∈ { x1, x2 } - la forme développée : f(x) = a x² + b x + c
pour le passage de (3/9 − 4/3) à −1, il manque la mise au même dénominateur :
3/9 − 4/3 = 3/9 − 12/9 = −9/9 = −1
forme 3 (forme factorisée) : Bien
puis appliquer les formules habituelles (si nécessaire)
3x² + 2x = 0 : factorisation immédiate : x (3x + 2) = 0
SOIT x = 0 : x1 = 0
SOIT 3x + 2 = 0 : x2 = −2/3
faire une seule opération à la fois
garder les parenthèses.
f(√2) = √2 (3 √2 − 1) + 1 (3√2 − 1)
calculons : √2 × 3 √2 = 3 (√2)² = 3×2 = 6
f(√2) = 6 − √2 + 3 √2 − 1
f(√2) = 5 + 2 √2
Pour calculer f(√2) : la forme la plus appropriée est la forme 2 (forme développée) :
f(√2) = 3 (√2)² + 2 √2 − 1
f(√2) = 3 ×2 + 2 √2 − 1
f(√2) = 6 + 2 √2 − 1
f(√2) = 5 + 2 √2
x + 1/3 = 0 soit f(x) minimum = 3(0)² − 4/3 = −4/3
valeur correspondante de x : x = −1/3
| x | −∞ | −1/3 | ∞ | ||
| f(x) | ↘ | −4/3 | ↗ | ||
le point (−2/3,−1) est obtenu par symétrie du point (0,−1) par rapport à l'axe de la parabole : x=−1/3
- une suite est une application de ℕ sur ℝ
souvent notée u(n) ou un au lieu de f(x) - définition explicite : u(n) = n² + 2n + 5 comme une fonction f(x) = x² + 2x + 5
Mais x ne prend que les valeurs entières n ∈ ℕ - définition par récurrence : on part d'une valeur u0
puis on applique une formule de récurrence : un+1 = f(un)
u0 → u1 → u2 → u3 → u4 → . . . jusqu'à l'infini - suite arithmétique : un+1 = un + r (où r est appelée la raison)
sa formule explicite est : un = u0 + n r
sa représentation graphique est une droite : y = r x + u0 (où x ne prend que les valeurs entières) - suite géométrique : un+1 = q un (où q est la raison)
sa formule explicite est : un = qn u0
sa représentation graphique est une exponentielle : u = u0 qx
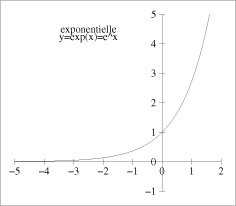
application : évolution des populations proportionnelle à la population
Habitants d'un pays,
Atomes radioactifs : n = nombre de périodes : N0 nombre initial
le nombre diminue de moitié à chaque période : N(n+1) = N(n) / 2
formule explicite : N(n) = N0 / 2n atomes restant radioactifs après n périodes - suite arithmético-géométrique : un+1 = q un + r
application : q = (1+τ) est l'augmentation dûe aux intérêts
r = remboursements mensuels
exemple capital emprunté = 10 000 euros ; taux d'intérêt = 5% ; remboursements annuels = 1000 euros
à la fin de la première année : le capital aura augmenté de 5% : 10 500 euros et on aura remboursé 1000 euros
Il restera 9 500 euros de capital à rembourser.
On répète le calcul pour l'année suivante . . . - calcul d'une racine carrée : voir Méthode de Héron d'Alexandrie
calcul de √a :
initialisation : u0 = 1
récurrence : un+1 = (1/2) ( un + a / un )
Calcul de √2 :
u0=1 ; f(x)=(x + 2/x) / 2 ; u(n+1) = f(u(n))
u(1) = 1.5
u(2) = 1.4166666666666665
u(3) = 1.4142156862745097
u(4) = 1.4142135623746899
u(5) = 1.414213562373095
u(6) = 1.414213562373095
convergence numérique : u(n+1) = u(n) = L
- suite de Fibonacci : voir Suite de Fibonacci
u0 = 1 ; u1 = 1 ; puis un+2 = un+1 + un
n=0 : u2 = u1 + u0 = 2
n=1 : u3 = u2 + u1 = 3
n=2 : u4 = u3 + u2 = 5
n=3 : u5 = u4 + u3 = 8
n=4 : u6 = u5 + u4 = 13
. . .