cours du 16/03/2021   (répertoire)

• vocabulaire : dans l'exercice 15 j'ai un doute quant à cocher la c)
   
• méthode :
  0) lire et relire plusieurs fois l'énoncé en notant les éléments importants
    50 % des erreurs viennent d'une mauvaise lecture de l'énoncé
    il faut utiliser toutes les données de l'énoncé
    et répondre à la question de l'énoncé
  1) écrire la formule générale du cours
  2) écrire la même formule appliquée avec les données de l'énoncé
  3) vérifier qu'on répond bien à la question de l'énoncé.
   
• sujet du bac 1S 2021 : n°02600 exercice 2
  Pour le 1) comment avez-vous vu que c'était une suite géométrique ?
  La première ligne du sujet de la partie A est :
  (U_n) est une suite géométrique de premier terme U₀ = 25 000 et de raison 0,94.
   
  Pour le 2) il fallait faire q-1n+1/1-q?
  La formule pour la somme de suite géométrique est S = U₀ (1 − qⁿ⁺¹) / (1 − q) = U₀ (qⁿ⁺¹ − 1) / (q − 1)
  où U₀ est le premier terme et n le nombre de termes
  7 termes : U₀ + U₁ + . . . + U₆ (cela fait 7 termes)
  Dans la première ligne de l'énoncé : de premier terme U₀
  Donc 7ème terme U₆
   
  Pour la 3) du coup j'ai eu aussi faux
  évidemment puisque vous n'avez pas pris les bonnes suites
   
  Pour la partie b comment vous avez vu le 0,94 c'est par rapport à la partie a ?
  partie B) types des suites ok
  quelles sont les raisons ? : diminution de 6% : x ---> x - (6/100)x = (94/100)x = 0,94 x
  la raison de la suite géométrique est 0,94
  à vous de continuer
  Attention on demande l'année :
  Il faut bien définir u₀ et v₀ et l'année correspondant à n=0
  puis en déduire n tel que v_n > u_n et reconvertir en année.
• attention, vous avez mal compris l'énoncé :
  (U_n) est une suite géométrique de premier terme U₀ = 25 000 et de raison 0,94.
  1) la formule explicite de U_n est donc U_n = U₀ qⁿ
  soit ici : U_n = 25 000 * 0,94ⁿ
  Remarque : une raison arithmétique aussi petite par rapport à U₀ était bizarre !
  2) somme des 7 premiers termes :
  Cela fait beaucoup de termes à calculer puis à additionner !
  Il vaut mieux employer la formule générale (si on est certain de la connaître)
  S = U₀ + . . . + U₆ (cela fait 7 termes)
  S = U₀ ( 1 + q + . . . + q₆ )
  qS = U₀ ( q + . . . + q₇ )
  (1 − q) S = U₀ ( 1 − q₇ )
  S = U₀ ( 1 − q₇ ) / (1 − q)
  Soit ici : S = 25000 * ( 1 − 0,94⁷) / (0,06) = 146467.6690864001
  3) V_n est défini dans l'énoncé : V_n = 50 ( 104 + 25 n)
  On donne le nom que l'on veut à une suite v_n = n (n+1) / 2 n'a rien à voir avec ce V_n
  Vous pouvez refaire tout l'exercice :
  Relire plusieurs l'énoncé pour être sûr de n'avoir pas oublié un mot (tous les mots sont importants)
• Suite Arithmético-Géométrique : u_n+1 = 0,7 u_n + 3000 avec u₁ = 8000
  a)
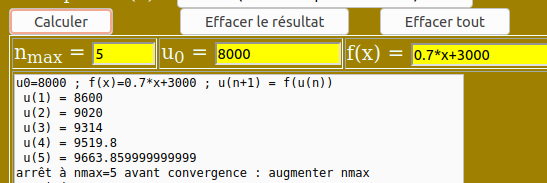
  attention : Vous avez écrit : 70% → 7/100 → 0,7 Il faut écrire : 70% → 70/100 ⇒ 0,7 (ou 0,70)
  u₁ = 8000 → u₂ = 8600 → u₃ = 9020 → u₄ = 9314 → u₅ = 9519,8 → u₆ = 9663,86 → . . .
   
  b) La formule qui est demandée est la formule de récurrence : u_n+1 = 0,7 u_n + 3000 avec u₁ = 8000
  elle n'est pas arithmétique car r = u_n+1 − u_n n'est pas constant (dépend de n)
  elle n'est pas géométrique car q = u_n+1 / u_n n'est pas constant (dépend de n)
  On le vérifie avec les 3 premiers termes :
  u₂ − u₁ = 600 et u₃ − u₂ = 420 donc pas de raison arithmétique
  de même u₂ / u₁ = 1,075 et u₃ / u₂ = 1,0488372093023255 différents donc pas de raison géométrique
   
  c) Voilà la suite auxiliaire v_n = u_n − L dont j'avais parlé. (au signe près)
  c.I) v₁ = 10000 − u₁ = 2000
    si la suite (v_n) est géométrique, sa raison est q = v_n+1/v_n
  Tout ce que l'on sait sur v_n, c'est sa définition : donc on le remplace par sa définition
  v_n+1 = 10 000 − u_n+1
  v_n+1 = 10 000 − (0,7 u_n + 3000)
  v_n+1 = 10 000 − 0,7 u_n − 3000
  v_n+1 = 7 000 − 0,7 u_n     Ici on va exprimer u_n en fonction de v_n
  v_n = 10 000 − u_n
  d'où u_n = 10 000 − v_n
  v_n+1 = 7 000 − 0,7 (10 000 − v_n)
  v_n+1 = 7 000 − 7 000 + 0,7 v_n
  v_n+1 = 0,7 v_n
   
  Explication de la méthode : en soustrayant la première ligne de la deuxième

  un+1	=	q un + r
  L	=	q L + r
  L − un+1	=	q (L − un)	soustraction
  vn+1	=	q vn

  avec L défini par : L = q L + r soit L = 0,7 L + 3000 donc L = 10 000
   
  c.II) (v_n) est géométrique, de raison q = 0,7 et de premier terme v₁ = 2000
  formule explicite : v_n = v₁ qⁿ⁻¹ = 2000 × 0,7ⁿ⁻¹
  puis : u_n = 10 000 − v_n = u_n = 10 000 − 2000 × 0,7ⁿ⁻¹
  u_n = 2000 ( 5 − 0,7ⁿ⁻¹ )

retour au menu :   cours 2020-2021   math 1ère S   math  
file:///home/jacques/Dropbox/