DM trigo.   (répertoire)

• sujet : Exercices trigonométrie 1SPE.pdf
• 1.1) Sens trigo : sens direct, sens inverse des aiguilles d'une montre.
• 1.2) Cercle trigo : rayon r=1 donc périmètre = 2 π r = 2 π
• 1.3) ? La longueur d'un segment est positive, de même que l'angle compté dans le sens trigo.
• 1.4) Pour que 2 points se superposent, leur distance doit être un multiple de 2 π
  dire que 2 points d'une droite sont distants d'un degré n'a pas de sens :
  sur la droite réelle, la distance est sans dimension (donc en "radian")
   
• exercice 2 : x ∈ [0;π] avec cos(x) = −0,8
• 2.1.a) I = tout le haut du cercle trigo (sinus ≥ 0)
• 2.1.b) tracer la verticale passant en −0,8
• 2.2) Calculatrice : fonction inverse de cosinus : arc-cosinus noté acos(0,8) = 2,498091544796509 ≈ 2,50
  Attention aux arrondis : la valeur la plus proche du nombre complet
  Attention aux unités de la calculatrice : vérifier que les angles sont bien en radians.
  autrement on obtient le résultat en degrés : 143,13°
• 2.3) On utilise la relation : sin²(x) + cos²(x) = 1
  sin²(x) = 1 − cos²(x) = 1 − 0,64 = 0,36
  sin(x) = √0,36 = 0,6
   
• 3.1) traits de construction : utilisation de la règle et du compas.
  
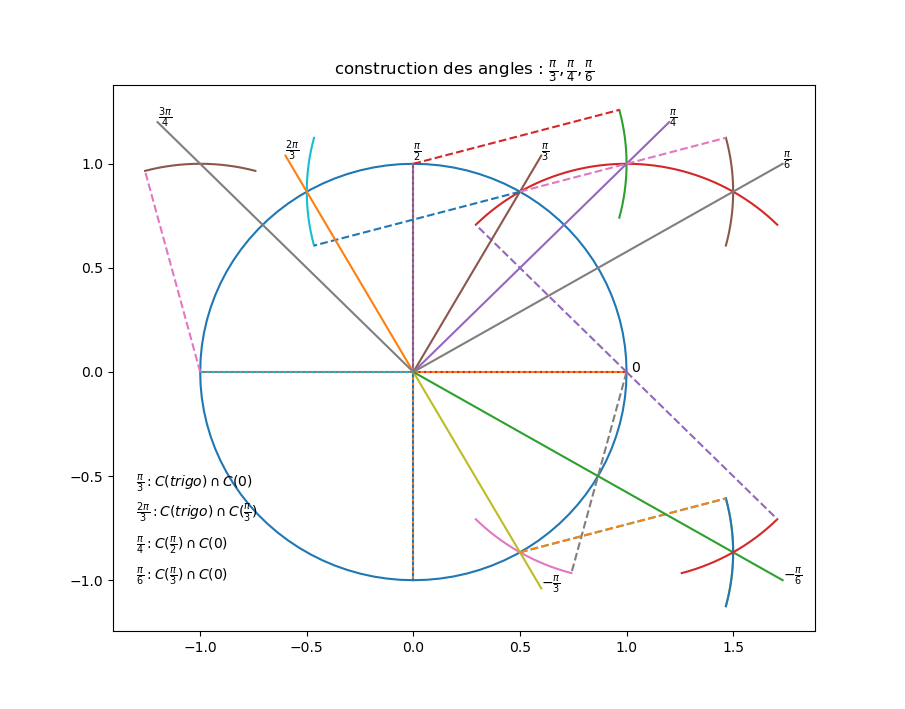
  en gardant l'ouverture du compas qui a servi à tracer le cercle trigo :
  • construction_angles.pdf   (au compas)
  • construction de π/2, −π/2 :
    d'abord, les angles de π/3 s'obtiennent en construisant des triangles équilatéraux :
    π/3 est obtenu par C(trigo) ∩ C(0)
    2π/3 est obtenu par C(trigo) ∩ C(π/3)
    enfin π/2 est obtenu par C(π/3) ∩ C(2π/3)   ( bissectrice de l'angle (π/3, 2π/3) )
  • construction de 3π/4 :
    un angle de 3π/4 (ou π/4) est la bissectrice de l'angle droit.
    3π/4 est obtenu par C(π/2) ∩ C(π)
  • construction de −π/6 :
    un angle de −π/6 (ou π/6) est la bissectrice de −π/3
    −π/3 est obtenu par C(trigo) ∩ C(0)
    −π/6 est obtenu par C(0) ∩ C(−π/3)
     
• 3.2) pas de difficulté particulière pour placer les angles.
  seul "piège" : l'encadrement doit inclure le point cos(0)=1 qui est le maximum pour le cos(x) dans I.
  cos(x) ∈ [cos(3π/4), cos(0)] ∪ [cos(−π/6), cos(0)]
  cos(x) ∈ [−√2/2, 1] ∪ [√3/2, 1]
  cos(x) ∈ [−√2/2, 1]

retour au menu :   cours 2020-2021   math 1ère S   math  
file:///home/jacques/Dropbox/