1.1) Compléter le cercle trigo et placez les points A(−π/3) et B(3π/4)
1.2) M ∈ I = [−π/3, 3π/4]
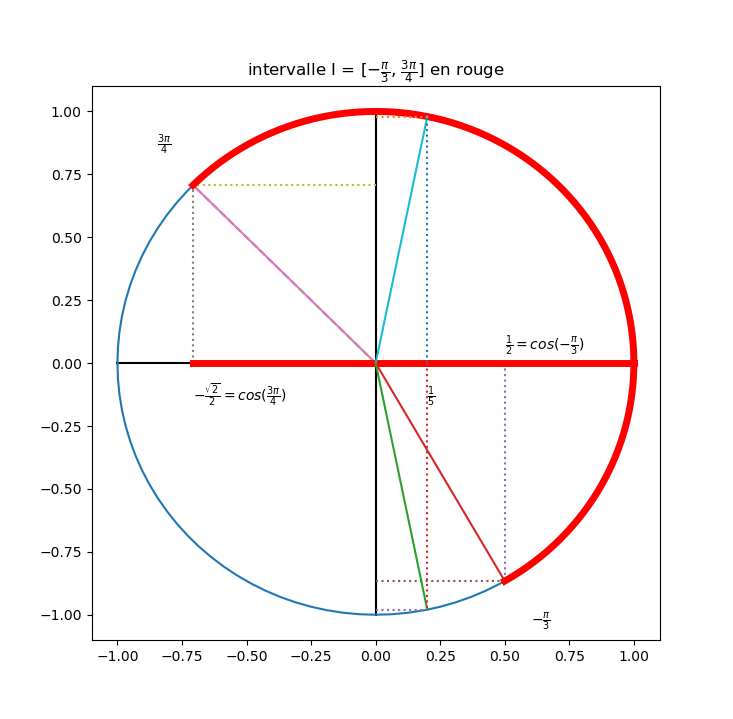
encadrement de cos(x) ∈ [−√2/2, 1]
ou bien −√2/2 ≤ cos(x) ≤ 1
1.3) cos(x) = 1/5
(sinx)² = 1 − 1/25 = 24/25
24 = 2² × 6 donc √24 = 2 √6
√24/25 = 2 √6 / 5
2 solutions sur le cercle trigo. complet : sin(x) = ± 2 √6
Solutions dans l'intervalle I :
il faut choisir le bon signe : en traçant la verticale cos(x)=1/5
on voit que l'angle correspondant au sinus −2 √6 est en dehors de l'intervalle.
Il n'y a donc qu'une solution dans I : sin(x) = + 2 √6
ATTENTION : pour un résultat en degrés,
sur la calculatrice mettre les angles en degrés sinon :
acos(1/5) = 1.369438406004566 radians
acos(1/5) = 78.46304096718453 ° ≈ 78.46° (au centième)
2.1) Il y a un seul lave-linge dont la valeur se déprécie chaque année.
première année : 510 − 510*15/100 = 433.5
deuxème année : 433.5 − 433.5*15/100 = 368.475
troisème année : 368.475 − 368.475*15/100 = 313.20375
2.2) Justifier que −15% équivaut à *0.85
Soit x la valeur du lave-linge : une réduction de 15% donne un nouveau prix :
x − x*15/100 = x (1 − 15/100) = x (85/100) = 0.85 x
une réduction de 15% équivaut à une multiplication par 0.85.
les valeurs remboursables forment une suite géométrique de raison 0.85
de premier terme : u0 = 510
2.3) valeur remboursable en 2020 :
nombre d'années : 2020−2014 = 6
ATTENTION à l'arrondi au centième :
valeur(2020) = 510 * 0.856 = 192.34625296874992 ≈ 192.35
3.1) image(−3) : f(−3) = 2
3.2) antécédents(0) : { −4 ; 1 ; 3 }
3.3) f(x) = −1 : x ∈ {−5 ; 1,3 ; 2,7 } valeurs approximatives
3.4) f(x) = 2 : il y 2 solutions à cette équation
3.5) le maximum de f(x) est atteint pour x = −1
3.6) résoudre f(x) >= 2 : x ∈ [ −3 ; 0 ] ou −3 ≤ x ≤ 0
3.7) le minimum de f(x) est −2
tableau de signe
| x | −5 | −4 | 1 | 3 | 4 | ||||
| f(x) | − | 0 | + | 0 | − | 0 | + | ||