cours du 01/06/2016 : ?

cours du 01/06/2016 : ? (répertoire)

loi binomiale B(n,p) (somme de n tirages de Bernoulli B(p))

Exercice 1 :

méthode de projection (quand on connaît les projections des points)
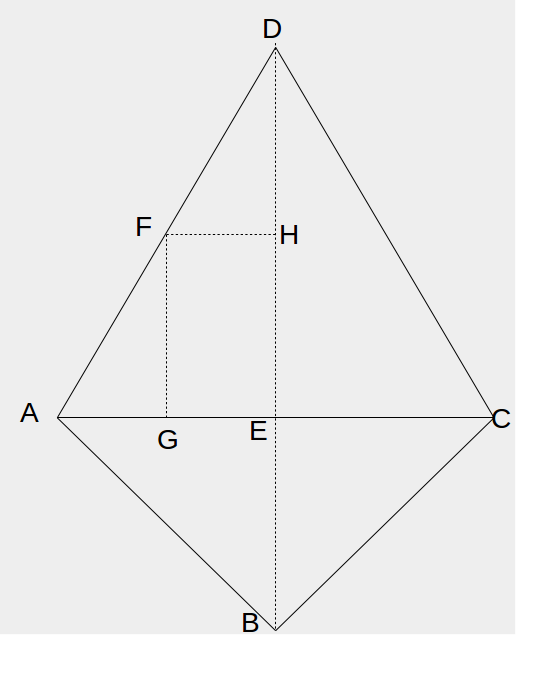
F milieu de AD ⇒ G milieu de AE et H milieu de ED
vect(AC) . vect(AF) = vect(AC) . vect(AG) = (1/4) AC²
vect(EC) . vect(CA) = − (1/2) AC²
vect(DB) . vect(AC) = vect(EE) . vect(AC) = 0 × 6 = 0
vect(AE) . vect(CB) = vect(AE) . vect(CE) = − (1/2) vect(AC) . (1/2) vect(AC) = − (1/4) AC²
vect(AF) . vect(ED) = vect(EH) . vect(ED) = (1/2) ED² = (1/2) (6² − 3²) = 27/2
vect(CA) . vect(AB) = vect(CA) . vect(AE) = − 6 × 3 = − 18

Exercice 1.1 :
DE : Dans le triangle ADE rectangle en E (les médianes d'un triangle équilatéral sont aussi hauteur) : Pythagore . . . → OK
AB : Dans le triangle ABC rectangle en B : Pythagore . . . 2 AB² = 36 → OK
→ mais ensuite : AB² = 18 et AB = 3 √2
remarque : si AB = 3 = BC alors comme AC = 6, AC = AB + BC : B serait au milieu de AC impossible
→ il faut savoir que la diagonale d'un carré de côté a vaut a √2 (d'après Pythagore).
Ici les côtés du carré sont AB et BC, on peut le terminer en ajoutant un point.
Exercice 1.2 :
1.2.a) vect(AC) . vect(AF) = 6 × 3 × cos(π/3) = 9 → OK
1.2.b) vect(EC) . vect(CA) = EC × CA × cos(EC,CA) = 3 × 6 × cos(π) = 18 × (−1) = −18 → OK
1.2.c) vect(DB) . vect(AC) = DB × AC × cos(π/2) OK
or cos(π/2) = 0 : inutile de calculer DB
→ vect(DB) . vect(AC) = DB × 6 × 0 = 0
sinon, pour calculer DB : DB = DE + EB
EB = 3 :
le triangle ABC peut être décomposé en 2 triangles rectangles isocèles AEB et BEC car ABC est un demi-carré
→ faire le dessin d'un carré avec ses 2 diagonales (perpendiculaires)
→ pour connaître le signe d'un produit scalaire, on regarde si les vecteurs sont dans le même sens ou de sens opposés.
Quand les vecteurs sont perpendiculaires, il ne sont ni dans le même sens, ni de sens opposés :
leur produit n'est ni positif, ni négatif : il est forcément nul.
1.2.d) vect(AE) . vect(CB) = 3 × 3 √2 × cos(5 π/4) = 3 × 3 √2 × (−1/√2) = −9
→ pour voir l'angle entre les vecteurs vect(AE) et vect(CB), il faut les faire partir d'un même point (centre du cercle trigo.)
1.2.e) vect(AF) . vect(ED) = AF × ED cos(30°) OK → = 3 × 3 √3 × √3/2 = 27/2 (= 13,5)
1.2.f) vect(CA) . vect(AB) = CA × AB × cos(CA,AB) = 6 × 3 √2 × cos(3 π/4) = 18 × √2 (−√2/2) = − 18
→ important à savoir : quand on fait un produit scalaire : vect(AB) . vect(AC)
vect(AB) . vect(AC) = AB × AC × cos(AB,AC)
Soit H la projection de C sur (AB) : AH = AC cos((AB,AC)
→ faire un dessin : donc le produit scalaire devient : vect(AB) . vect(AH) où les vecteurs sont colinéaires.
Voici l'exercice en projetant un des 2 vecteurs sur l'autre :
1.2.a) vect(AC) . vect(AF) = 1,5 × 6 = 9 (en projetant F au milieu de AE)
1.2.b) vect(EC) . vect(CA) = − 3 × 6 = − 18 (pas de projection à faire)
1.2.c) vect(DB) . vect(AC) = 0 × 6 D et B se projettent en E : la projection de DB sur (AC) = 0
1.2.d) vect(AE) . vect(CB) = vect(AE) . vect(CE) = −9 B se projette en E sur (AC)
1.2.e) vect(AF) . vect(ED) = vect(ED)/2 . vect(ED) = 27/2 A se projette en E et F se projette au milieu de ED
1.2.f) vect(CA) . vect(AB) = vect(CA) . vect(AE) = − 6 × 3 = −18
C'est plus simple donc plus sûr. → entraîne-toi avec cette méthode.

cours :

avec le vecteur projeté :
A------H----------------B
 \     |
  \    |
   \   |
    \  |
     \ |
      \|
       C
vect(AB) . vect(AC) = vect(AB) . vect(AH)
car AH = AC cos(HAC)
définition du cosinus : cos(HAC) = adjacent / hypoténuse
cos(HAC) = AH / AC
AH = AC cos(HAC)

signe du produit scalaire : vect(AB) . vect(DC)

                            C
                             \
A-----------------------B     \
                               \
                                \
                                 \
                                  D
Mettre les origines A et D au même endroit : O = A' = D'
C'
 \
  \
   \
    \
     \
      O-----------------------B'
On voit que l'angle (AB,DC) > π/2 (donc son cosinus est < 0)

Exercice 2 :
2.1) droite perpendiculaire au vect(n) = (2;−1) et passant par A (1;−2)
→ nx x + ny y = nx xa + ny ya 2 x + (−1) y = 2 × 1 + (−1) × (−2) = 4 2 x − y − 4 = 0
2.2) D : 2 x + y + 3 = 0 droite perpendiculaire : n = (−1;2) donc (−1) x + 2 y = (−1) xb + 2 yb
2.3) C : (x −x0)² + (x − x0)² = r² (x −(−2))² + (x − 3)² = 3² (x + 2)² + (x − 3)² = 9
2.4) centre milieu de AB = (1/3+3/2;−1+5/6) = ((2+9)/6;(−6+5)/6) = (11/6;−1/6)
r² = (2/3 − 11/6)² + (−2 − (−1/6))² = (4/6 − 11/6)² + (−12/6 + 1/6)² = (−7/6)² + (−11/6)² = (49 + 121)/36 = 170/36
(x − 11/6)² + (y + 1/6)² = 170/36
(6 x − 11)² + (6 y + 1)² = 170
vérif. A et B appartiennent au cercle:
(6 × 2/3 − 11)² + (6 × (−2) + 1)² = 170
(6 × 3 − 11)² + (6 × 5/3 + 1)² = 170
exercice 3
3.1) x² + y² + 2 x − 6 y + 5 = 0
(x + 1)² = x² + 2 x + 1
(y − 3)² = y² − 6 y + 9
(x + 1)² + (y − 3)² = x² + y² + 2 x − 6 y + 10 = 5
(x + 1)² + (y − 3)² = 5
centre I (−1 ; 3) rayon √5
3.2) intersection avec y = 0 : (x + 1)² + (3)² = 5 (x + 1)² = −4 impossible
intersection avec x = 0 : 1 + (y − 3)² = 5
(y − 3)² − 4 = 0
y − 3 = 2 => y = 5 soit B (0 ; 5)
y − 3 = −2 => y = 1 soit A (0 ; 1)
AB (0 ; 4)
3.3) la tangente au cercle en A est perpendiculaire au vecteur AI (−1 − 0 ; 3 − 1) = (−1 ; 2)
(−1) x + 2 y = (−1) × 0 + 2 × 1 = 2
−x + 2 y − 2 = 0
3.4) angle IAB : cos(IAB) ?
AI . AB = √5 × 4 × cos(IAB) = 8
cos(IAB) = 2 / √5
l'angle IAB est dans l'intervalle [0;π/2]
IAB = 26.56505117707799 ° environ 26,6 °
IAB = 0.46364760900080615 rad (environ 0,5 rad)

retour au menu : cours 2015 math 1ère S math