Cours du 07 Mai 2011

• C'est intéressant de relire le compte-rendu de langues de l'ESSEC
  Car souvent, on ne sait pas ce qu'attendent les correcteurs.
  Ils disent aussi quelles sont les plus grosses erreurs à éviter.
• Pascal : Pascal page 2 et Pascal page 3 de mon cours
• Equivalence : f(x) ∼ g(x) au voisinage de x₀
  • Si : limite quand x → x₀ de f(x) / g(x) = 1
  • Cas particulier : si limite quand x → x₀ de f(x) = L , alors f(x) ∼ L
  • si x₀ ≠ ± ∞ : f(x) = f(x₀) + f '(x₀) x     ( si la fonction est définie et dérivable en x₀ )
    • Si f(x₀) ≠ 0 : f(x) ∼ f(x₀)
    • Si f(x₀) = 0 : f(x) ∼ f '(x₀) (x − x₀)
    • Si f(x₀) = 0 et f '(x₀) = 0 : f(x) ∼ f ''(x₀)/2! (x − x₀)²
    • ... on prend le premier terme non nul du développement limité
  • Equivalence d'une somme f₁(x) + f₂(x) : on met en facteur le plus grand terme (en valeur absolue)
    • au voisinage de 0 : (x + 1) ∼ 1
    • au voisinage de 0 : (x + x²) = x (1 + x) ∼ x × 1 ∼ x
    • → Classement des termes au voisinage de 0 :
      1/x² >> 1/x >> 1/√x >> 1 >> √x >> x >> x²
      Remarque : Le classement des inverses est symétrique par rapport à 1
      >> signifie très supérieur, ici infiniment supérieur : dans une somme on ne garde que le terme infiniment supérieur
    • au voisinage de +∞ : (x + 1) = x(1 + 1/x) ∼ x
    • au voisinage de +∞ : (x + x²) = x² (1/x + 1) ∼ x² × 1 ∼ x²
    • → Classement des termes au voisinage de +∞ :
      e^x >> x² >> x >> √x = x^1/2 >> ln(x) >> 1 >> 1/ln(x) >> 1/√x = x^−1/2 >> 1/x = x⁻¹ > 1/x² = x⁻² >> 1/e^x = e^−x
      Remarque : Pour les puissances, c'est le classement inverse du voisinage de 0
  • Equivalence d'un produit f₁(x) × f₂(x) : on fait le produit des équivalents
    • Exemple : (x + 1) × (x² + 2 x + 1)
    • au voisinage de 0 : (x + 1) × (x² + 2 x + 1) ∼ 1 × 1 ∼ 1
    • au voisinage de +∞ : (x + 1) × (x² + 2 x + 1) ∼ x × x² ∼ x³
  • applications : équivalence au voisinage de 0
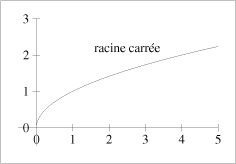
    • f(x) = √x → 0, mais n'est pas dérivable en 0 car sa dérivée est infinie en 0 ( f '(x) = 1 / (2 √x) )
      
    • f(x) = e^x ∼ 1
    • √x = x^1/2 est un terme simple
    • √x / (1 + x) ∼ √x / x = 1 / √x
    • f(x) = x e^2x ∼ x × 1 ∼ x
      remarque : f '(x) = e^2x + x × 2 e^2x   =>   f '(0) = 1   donc :   f(x) ∼ f '(0) x ∼ x
    • f(x) = (1/x) ln( (1+x) / (1−x) ) = (1/x) [ ln(1+x) − ln(1−x) ]
      étude du terme : g(x) = [ ln(1+x) − ln(1−x) ]
      g'(x) = 1/(1+x) − −1/(1−x) = [ (1−x) + (1+x) ] / (1 − x²) = 2 / (1 − x²)
      g'(0) = 2 => g(x) ∼ 2 x
      d'où : f(x) ∼ 2 x / x = 2
    • f(x) = (1+x)^x → 1⁰ = 1   donc : (1+x)^x ∼ 1
    • limite de f(x) = (1+x)^1/x quand x → 0
      • ln(f(x)) = (1/x) ln(1+x)
      • ln(1+x) ∼ x   car : ln(1) = 0 et ln(1+x)' = 1/(1+x) = 1 pour x=0
      • ln(f(x)) ∼ (1/x) x = 1
      • limite de f(x) = e¹ = e
• Algèbre linéaire :
  • indépendance des vecteurs d'une famille { x_i } pour i appartient à [[1 ; n ]]
    si ∑_i a_i x_i = 0 => a_i = 0
  • Une famille libre de n vecteurs engendre un sous-espace vectoriel de dimension n
  • résolution du système : ∑_i a_i x_i = 0 par triangularisation
  • Si le sytème peut être triangularisé avec tous les termes diagonaux ≠ 0, alors les vecteurs sont libres.
  • Si un terme diagonal = 0, alors les vecteurs sont liés
  • Il y a autant de vecteurs "inutiles" que de lignes nulles. (On peut les exprimer en fonction des autres)
  • La dimension de l'espace engendré est égale au nombre de lignes non nulles.

retour aux menus :   cours   prépa HEC