cours du 07/10/2015     (répertoire)

• calculer les points d'une courbe :
  • mode d'emploi de la Casio 35+  
    (comme c'est un fichier pdf, on peut rechercher un texte avec [Ctrl F] "texte à rechercher")
  • Quand la calculatrice a un comportement bizarre : Réinitialiser les réglages de configuration
    [MENU] [SYSTEM] [F5:réinitialisation] [F1:Données Config] (remarque : revient en mode radian)
  • Mode degré/radian : [MENU] [RUN MATH] [SET UP] Angle : Rad / Deg [EXIT]
    ([SET UP] = [SHIFT] + [MENU])
  • Régler le contraste : [MENU] [F1:Contraste] régler le contraste avec les flèches ← → [MENU]
• DS exercice 2 question A2 : Δ = (−6)² − 4 × 1 × m
  • simplifier le résultat : Δ = 36 − 4 m
  • résoudre Δ(m) = 0 : m = 36/4 = 9
    faire un tableau de signe de Δ(m) :     (← on résoud les 3 cas en même temps)
    Δ(m) est du signe de (−4) quand m → +∞

    m	−∞	9	+∞
    Δ(m)	+	0	−
    nombre de racines	2	1	0

    remarque : ces résultats sont cohérents avec ceux calculés précédemment : m ∈ {0, 4, 15}
  • ou bien : résoudre pour 2 racines : Δ(m) > 0
    • 36 − 4 m > 0
    • − 4 m > − 36
    • m < − 36 / (− 4) = 9     (attention : changement de sens car on divise par un nombre < 0)
    • Puis pour 1 racine : Δ(m) = 0
    • Puis pour 0 racine : Δ(m) < 0
• Fin du devoir surveillé :
  • exercice 3 question 3 : d(v) = (1/5) v + (1/150) v² ≤ 12 mètres
    • on peut résoudre : (1/5) v + (1/150) v² = 12 pour obtenir la vitesse limite.
      (1/150) v² + (1/5) v − 12 = 0
      Δ = b² − 4 a c = 1/25 − 4 (1/150) (− 12) = 0,36
      x = (−b ±√Δ) / (2 a) = (−1/5 ±√0,36) / (2/150)
      x ∈ {−60, 30} : x limite = 30 km/h
    • ensuite dire que la vitesse doit être inférieure à cette limite pour que la distance soit plus courte
      v ≤ 30 km/h     (résultat de bon sens)
    • mieux : on peut faire un tableau de signe pour d(v) − 12 ≤ 0 ; éliminer la partie v < 0
      les parties à conserver sont en vert

      v	−∞	−60		0		30	+∞
      v	−	−	−	0	+	+	+
      d(v)−12	+	0	−	−	−	0	+
      v > 0 et d < 12

      0 ≤ v ≤ 30 km/h    (toujours vérifier qu'un résultat de calcul n'est pas absurde)
  • exercice 4 question 1 :
    s'entraîner à suivre une courbe pour trouver les valeurs des points particuliers
  • exercice 4 question 2 :
    il n'y a pas une conclusion unique. (il faut deviner ce qu'attend le prof.)
    par contre, il faut dire : la solution exacte est [−2/3 ; 2]
    on peut dire que [−0,7 ; 2] est faux.   (← plus simple)
    on peut dire que [−0,7 ; 2] est approximatif (à la précision 10⁻¹ près).
• Optique : images virtuelles
  • image réelle : les rayons lumineux passent réellement par l'image (on peut la voir sur un écran)
    une image réelle est située après la lentille (à droite)
  • image virtuelle : les rayons lumineux semblent provenir de l'image.
    une image virtuelle est située avant la lentille (à gauche)
    Les rayons lunimeux ne passent pas par l'image : il faut prolonger les rayons (en pointillés)
  • Les rayons lumineux ne passent pas toujours réellement par les foyers : C'est leur prolongement qui passe par les foyers.
  • l'objet AB a grossir est entre le foyer objet F et la lentille O.
    l'image A'B' grossie est virtuelle. L'observateur situé à droite, il voit l'objet AB sous la forme A'B'.
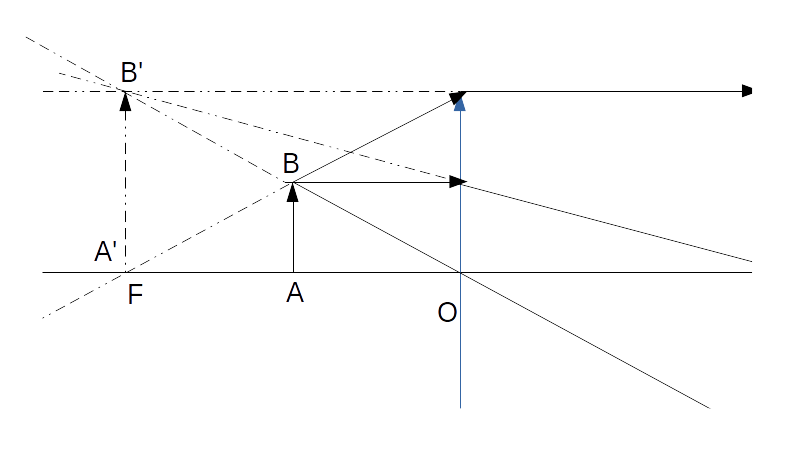
    Comme j'ai mis AB en OF/2, l'image est exactement en F (mais c'est un cas particulier)
• révisions du cours de l'année dernière : jusqu'au 01 Octobre 2014
  • révisions
  • asymptotes
  • limites
  • variations

retour au menu :   cours 2015   math 1ère S   math